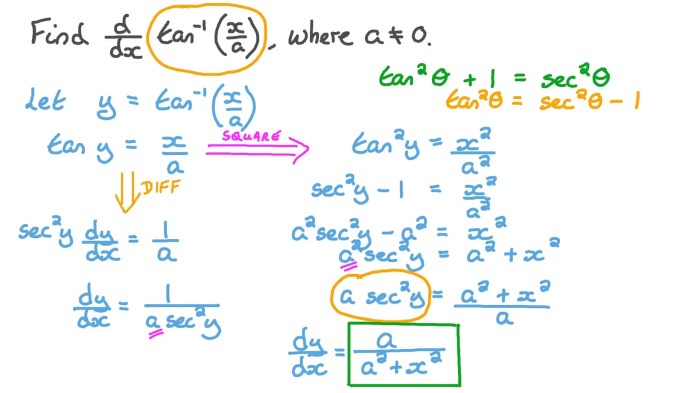
Differentiating inverse functions quiz ap classroom – Welcome to the realm of inverse functions, where the order of operations flips! In this engaging exploration, we’ll delve into the intricacies of differentiating inverse functions, equipping you with a powerful tool for solving real-world problems. Get ready to unravel the mysteries of inverse functions and conquer the AP Classroom quiz with confidence.
Differentiating Inverse Functions: Differentiating Inverse Functions Quiz Ap Classroom

Inverse functions are functions that undo each other. If f(x) is a function, then its inverse function, f^-1(x), is the function that satisfies the equation f(f^-1(x)) = x and f^-1(f(x)) = x.The graph of an inverse function is the reflection of the graph of the original function over the line y = x.Inverse
functions have a number of properties. For example, the inverse of a one-to-one function is also one-to-one. The inverse of a continuous function is also continuous. And the inverse of a differentiable function is also differentiable.
Differentiating Inverse Functions, Differentiating inverse functions quiz ap classroom
The chain rule can be used to differentiate inverse functions. The chain rule states that if f(x) is a function and g(x) is a function, then the derivative of f(g(x)) is given by the product of the derivative of f(x) and the derivative of g(x).In
other words,“`d/dx f(g(x)) = f'(g(x))
g'(x)
“`To differentiate an inverse function, we can use the chain rule with f(x) = x and g(x) = f^-1(x). This gives us the following:“`d/dx f^-1(x) = 1 / f'(f^-1(x))“`
Applications of Differentiating Inverse Functions
Differentiating inverse functions can be used to solve a variety of problems. For example, inverse functions can be used to find the velocity of an object given its position function. Inverse functions can also be used to find the concentration of a chemical given its reaction rate.Here
are some examples of how differentiating inverse functions can be used in various fields:
- Physics:Inverse functions can be used to find the velocity of an object given its position function.
- Economics:Inverse functions can be used to find the price of a good given its demand function.
- Biology:Inverse functions can be used to find the concentration of a chemical given its reaction rate.
Quiz on Differentiating Inverse Functions
Multiple-choice questions
Which of the following is the inverse function of f(x) = x^2?
(a) f^-1(x) = sqrt(x)(b) f^-1(x) =
sqrt(x)
(c) f^-1(x) = 1/x(d) f^-1(x) = x^3
What is the derivative of f^-1(x) = ln(x)?
(a) 1/x(b) x(c) ln(x)(d) 1/ln(x)Open-ended problems
- Find the inverse function of f(x) = e^x.
- Use the chain rule to differentiate f^-1(x) = sin(x).
- A ball is thrown into the air with an initial velocity of 10 m/s. The height of the ball is given by the function h(t) =
- 4.9t^2 + 10t. Find the velocity of the ball at time t = 2 seconds.
Questions Often Asked
What is the chain rule for differentiating inverse functions?
The chain rule states that if f is a differentiable function and g is its inverse, then the derivative of g with respect to x is given by dg/dx = 1/df/dg^-1(x).
How do I apply the chain rule to differentiate inverse functions?
To differentiate an inverse function, first find the derivative of the original function f. Then, substitute g^-1(x) for x in the derivative of f and multiply the result by -1.
What are some applications of differentiating inverse functions?
Differentiating inverse functions has applications in various fields, including physics (e.g., calculating velocity from position), economics (e.g., finding marginal revenue from demand), and biology (e.g., modeling population growth).