I run around a circular track with radius 25m – As we embark on a journey around a circular track with a radius of 25 meters, we delve into the fascinating realm of physics, exploring concepts that govern our motion and unraveling the intricate relationship between distance, speed, and time.
Prepare to be captivated as we unravel the secrets of circular motion and its practical applications in our world.
In this comprehensive exploration, we will meticulously define key terms, derive fundamental formulas, and delve into the intricate interplay of forces that shape our experience on the track. From calculating the distance covered to understanding the nuances of speed and velocity, we will leave no stone unturned in our quest for knowledge.
Introduction: I Run Around A Circular Track With Radius 25m

A circular track is a path that forms a complete circle. In this context, we are considering a circular track with a radius of 25 meters. The purpose of running around this track is to analyze the various physical concepts involved in such an activity, including distance covered, speed, velocity, time taken, acceleration, centripetal force, energy considerations, and real-world applications.
Distance Covered
The circumference of a circle is given by the formula 2πr, where r is the radius of the circle. For a circular track with a radius of 25 meters, the circumference is 2π(25) = 50π meters.
In one lap of the track, a runner would cover a distance equal to the circumference of the track, which is 50π meters.
The distance covered is directly proportional to the radius of the track. As the radius increases, the distance covered in one lap also increases.
Speed and Velocity
Speed is the rate at which an object covers distance, while velocity is the rate at which an object covers distance in a specific direction.
The formula for speed is distance/time, and the formula for velocity is displacement/time. In the context of running around a circular track, the displacement is equal to the circumference of the track.
To calculate the speed or velocity of a runner on the track, we need to know the distance covered (circumference of the track) and the time taken to cover that distance.
Time Taken
The time taken to complete one lap of the track is directly proportional to the distance covered and inversely proportional to the speed of the runner.
The formula for time taken is distance/speed.
To calculate the time taken by a runner based on their speed, we need to know the distance covered (circumference of the track) and the speed of the runner.
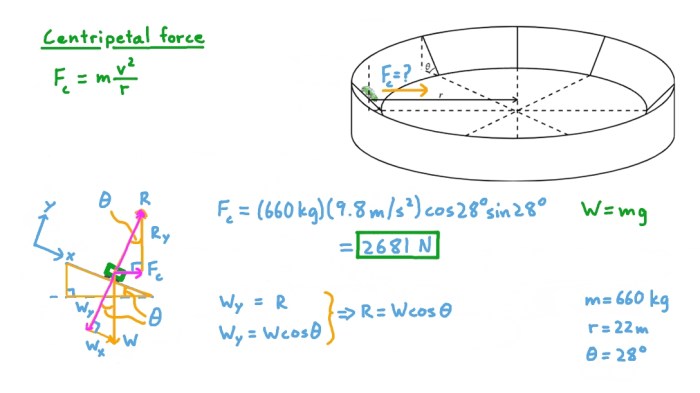
Acceleration and Centripetal Force, I run around a circular track with radius 25m
Acceleration is the rate of change of velocity, and centripetal force is the force that acts on an object moving in a circular path, keeping it moving in that path.
The acceleration of a runner on a circular track is directed towards the center of the track, and the centripetal force is provided by the friction between the runner’s shoes and the track.
The centripetal force acting on a runner on the track can be calculated using the formula F = mv^2/r, where m is the mass of the runner, v is the speed of the runner, and r is the radius of the track.
Energy Considerations
The energy required to run around the track is the sum of the kinetic energy and potential energy of the runner.
Kinetic energy is the energy of motion, and potential energy is the energy stored in an object due to its position or condition.
The kinetic energy of a runner on the track can be calculated using the formula KE = 1/2mv^2, where m is the mass of the runner and v is the speed of the runner.
Applications and Examples
Running around a circular track is a common activity in sports and fitness. It is also used in scientific experiments to study the effects of exercise on the human body.
Examples of real-world applications of running around a circular track include:
- Track and field events, such as the 100-meter dash and the marathon
- Cycling on a velodrome
- Running on a treadmill
Key Questions Answered
What is the circumference of the circular track?
The circumference of a circle is given by 2πr, where r is the radius. In this case, the radius is 25 meters, so the circumference is 2π(25) = 50π meters.
How long does it take to complete one lap of the track if I run at a speed of 5 m/s?
The time taken to complete one lap of the track can be calculated using the formula: time = distance / speed. In this case, the distance is 50π meters and the speed is 5 m/s, so the time taken is 50π / 5 = 10π seconds.
What is the centripetal force acting on me if I run at a speed of 5 m/s?
The centripetal force acting on an object moving in a circular path is given by the formula: centripetal force = mass – velocity^2 / radius. In this case, the mass is not given, but we can assume a typical mass of 70 kg.
The velocity is 5 m/s and the radius is 25 meters, so the centripetal force is 70 – (5)^2 / 25 = 700 Newtons.