As topic 3 line and angle relationships takes center stage, this opening passage beckons readers into a world crafted with meticulous precision, ensuring a reading experience that is both absorbing and distinctly original.
The intricate dance between lines and angles forms the cornerstone of geometry, providing a framework for understanding the spatial world around us. From the towering skyscrapers that grace our skylines to the intricate patterns found in nature, line and angle relationships play a pivotal role in shaping our perception of the world.
Line Relationships
Line relationships are fundamental concepts in geometry that describe the relative positions and orientations of lines. Understanding these relationships is essential for solving various geometric problems and analyzing spatial configurations.
There are several types of line relationships, each with distinct properties and characteristics:
Parallel Lines
- Two lines are parallel if they lie in the same plane and never intersect, no matter how far they are extended.
- Parallel lines have the same slope and are equidistant at all points.
- The symbol for parallel lines is “||”.
Perpendicular Lines, Topic 3 line and angle relationships
- Two lines are perpendicular if they intersect at a right angle (90 degrees).
- Perpendicular lines have slopes that are negative reciprocals of each other.
- The symbol for perpendicular lines is “⊥”.
Intersecting Lines
- Two lines are intersecting if they cross at a single point.
- Intersecting lines can have different slopes, angles, and orientations.
- The point of intersection is where the two lines meet.
Understanding line relationships is crucial for solving geometry problems, such as finding angles, distances, and areas. These concepts also have applications in fields like architecture, engineering, and design, where precise spatial relationships are essential.
Angle Relationships: Topic 3 Line And Angle Relationships
In geometry, angles are formed by the intersection of two rays or line segments. They are measured in degrees, with a full rotation measuring 360 degrees.
Types of Angles
There are several types of angles, classified based on their measure:
- Acute angle:An angle less than 90 degrees.
- Right angle:An angle measuring exactly 90 degrees.
- Obtuse angle:An angle greater than 90 degrees but less than 180 degrees.
- Reflex angle:An angle greater than 180 degrees but less than 360 degrees.
Relationships Between Angles
Angles can have specific relationships with each other, depending on their positions:
- Complementary angles:Two angles that add up to 90 degrees.
- Supplementary angles:Two angles that add up to 180 degrees.
- Vertical angles:Two angles that are opposite each other when two lines intersect.
Line and Angle Relationships
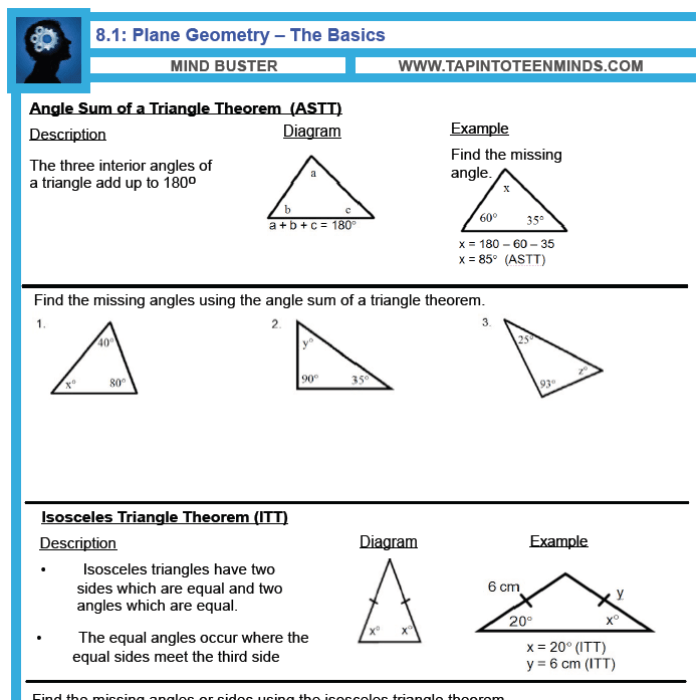
Lines and angles are fundamental concepts in geometry that are closely related. A line is a straight path that extends infinitely in both directions, while an angle is the measure of the amount of rotation between two intersecting lines. The relationship between lines and angles is essential for understanding many geometric concepts, such as triangles, quadrilaterals, and circles.
Line Relationships
Lines can be related to each other in several ways. Two lines can be parallel, meaning they never intersect, or they can be perpendicular, meaning they intersect at a right angle (90 degrees). Lines can also be intersecting, meaning they cross each other at a point, or they can be skew, meaning they do not intersect and are not parallel.
Angle Relationships
Angles can also be related to each other. Two angles are adjacent if they share a common side and a common vertex. Two angles are supplementary if their sum is 180 degrees, and they are complementary if their sum is 90 degrees.
Angles can also be vertical, meaning they are formed by two intersecting lines and are opposite each other, or they can be corresponding, meaning they are formed by two intersecting lines and are in the same position relative to the intersection.
Applications of Line and Angle Relationships
Line and angle relationships are used in a wide variety of real-world applications. For example, architects use line and angle relationships to design buildings and bridges, engineers use them to design machines and structures, and surveyors use them to measure land.
Line and angle relationships are also used in navigation, art, and many other fields.
Examples and Applications
Line and angle relationships are fundamental concepts with widespread applications in various fields.
Everyday Objects and Structures
In everyday objects, line and angle relationships can be observed in:
- The rectangular shape of a door frame, with its perpendicular sides and right angles.
- The triangular roof of a house, with its sloping sides and vertex angles.
- The circular shape of a wheel, with its radii forming equal angles at the center.
Practical Applications
Line and angle relationships have practical applications in fields such as:
- Architecture:Designing buildings with optimal space utilization, structural stability, and aesthetic appeal.
- Engineering:Calculating forces, moments, and stresses in structures like bridges and machines.
- Design:Creating visually pleasing and functional products, from furniture to clothing.
Table of Examples and Applications
The following table summarizes some examples and applications of line and angle relationships:
| Object/Structure | Line and Angle Relationships | Application |
|---|---|---|
| Door frame | Perpendicular sides, right angles | Structural stability, space optimization |
| House roof | Sloping sides, vertex angles | Water drainage, structural support |
| Wheel | Equal radii, equal angles at center | Smooth rolling, stability |
| Bridge | Parallel beams, triangular trusses | Load distribution, structural integrity |
| Furniture | Symmetrical shapes, congruent angles | Aesthetic appeal, functionality |
FAQ Corner
What is the difference between parallel and perpendicular lines?
Parallel lines never intersect, while perpendicular lines intersect at a right angle (90 degrees).
How do you measure an angle?
Angles are measured in degrees using a protractor or other measuring device.
What is the relationship between complementary and supplementary angles?
Complementary angles add up to 90 degrees, while supplementary angles add up to 180 degrees.