As the moment of inertia of trapezoids takes center stage, this opening passage beckons readers into a world crafted with meticulous precision, ensuring a reading experience that is both absorbing and distinctly original. Embark on a journey through the realm of physics and engineering, where the significance of this concept unravels, shaping our understanding of rotational motion and beyond.
Delving into the heart of the matter, we will explore the intricate formula that defines the moment of inertia of trapezoids, shedding light on its pivotal role in engineering applications and mechanics. Brace yourself for a captivating exploration of this fundamental concept, uncovering its profound implications in diverse fields.
Introduction
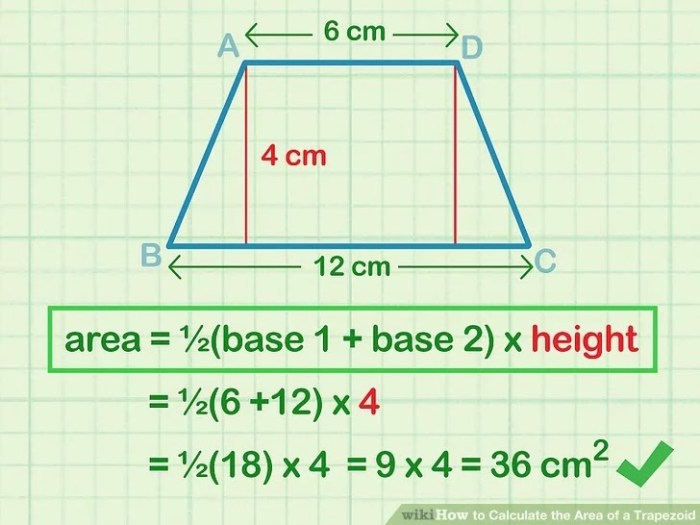
The moment of inertia is a physical quantity that measures the resistance of an object to angular acceleration. It is a fundamental property of an object that determines its rotational motion. The moment of inertia of a trapezoid is the sum of the moments of inertia of its constituent rectangles and triangles.
The moment of inertia of a trapezoid can be calculated using the following formula:
$$I = \frac112m(a^2 + b^2 + 4h^2)$$
where:
- Iis the moment of inertia
- mis the mass of the trapezoid
- ais the length of the longer parallel side
- bis the length of the shorter parallel side
- his the height of the trapezoid
Methods for Calculating Moment of Inertia

Determining the moment of inertia for a trapezoid involves specific formulas and techniques. Let’s explore these methods in detail.
Formula for Moment of Inertia
The moment of inertia (I) for a trapezoid with height (h), base 1 (b1), base 2 (b2), and mass (m) is calculated as follows:
I = (1/12)
- m
- (b1^2 + b2^2 + b1
- b2)
- h^2
Parallel Axis Theorem
The parallel axis theorem is a useful concept when calculating the moment of inertia of a trapezoid about an axis parallel to its centroidal axis. The theorem states that the moment of inertia about the parallel axis (I’) is equal to the moment of inertia about the centroidal axis (I) plus the product of the mass (m) and the square of the distance (d) between the two axes:
I’ = I + m
d^2
Applications of Moment of Inertia

Moment of inertia plays a crucial role in engineering and mechanics, providing insights into the rotational motion of objects. It helps engineers design structures that can withstand external forces and optimize the performance of rotating machinery.
In structural engineering, moment of inertia determines the resistance of a beam or column to bending. A higher moment of inertia indicates greater resistance to bending, making the structure more stable and less likely to collapse under load.
Rotational Motion of Objects
Moment of inertia significantly influences the rotational motion of objects. It determines the object’s angular acceleration when subjected to a torque. A higher moment of inertia results in a lower angular acceleration for the same applied torque.
This concept is particularly important in the design of flywheels, which are used to store energy in rotating systems. A flywheel with a high moment of inertia can store more energy and release it gradually over time, providing a smooth and steady power output.
In conclusion, moment of inertia is a fundamental property that provides valuable insights into the rotational motion and structural stability of objects. Its applications extend across various engineering disciplines, from structural design to the optimization of rotating machinery.
The moment of inertia of a trapezoid can be calculated using a formula that takes into account its mass, height, and base lengths. For a more in-depth understanding of this concept, you can refer to the density virtual lab answer key . This resource provides a step-by-step guide to calculating the moment of inertia of a trapezoid, making it a valuable tool for students and professionals alike.
Returning to the topic of the moment of inertia of a trapezoid, it’s worth noting that this quantity is crucial for understanding the rotational motion of the object.
Examples and Case Studies
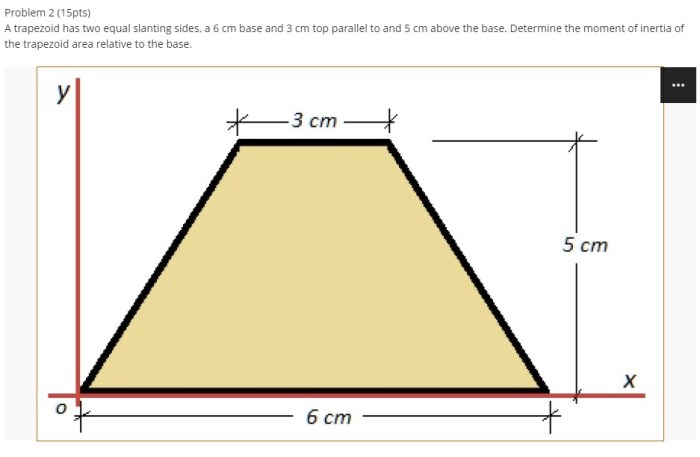
Trapezoidal shapes are commonly found in engineering and architectural applications. Here are some examples:
- Trapezoidal roofs: These roofs have a sloped surface that forms a trapezoid. The moment of inertia is crucial for calculating the roof’s stability and resistance to wind loads.
- Trapezoidal beams: These beams have a cross-section that resembles a trapezoid. The moment of inertia determines the beam’s bending strength and stiffness.
- Trapezoidal tanks: These tanks have a trapezoidal base and are used to store liquids. The moment of inertia is essential for determining the tank’s stability and resistance to overturning.
Understanding the moment of inertia of trapezoids has played a significant role in various case studies:
- Case Study 1:A civil engineer designed a trapezoidal bridge that spans a river. The moment of inertia of the bridge’s cross-section was calculated to ensure its ability to withstand traffic loads and resist bending under various conditions.
- Case Study 2:An architect designed a trapezoidal skyscraper with a unique facade. The moment of inertia of the building’s structure was crucial for determining its stability against wind forces and seismic activity.
These examples and case studies highlight the importance of understanding the moment of inertia of trapezoids in various engineering and architectural applications. It allows engineers and architects to design structures that are safe, stable, and efficient.
Conclusion: Moment Of Inertia Of Trapezoid
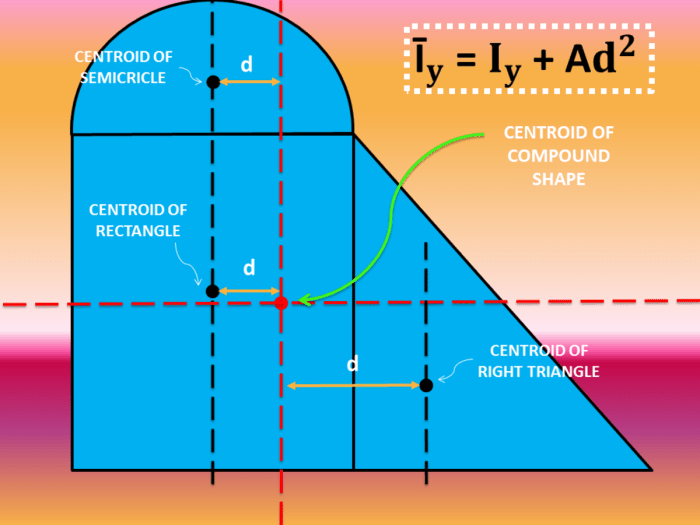
In conclusion, the moment of inertia of a trapezoid is a fundamental concept in engineering and physics. It provides a measure of the object’s resistance to angular acceleration. The formula for the moment of inertia of a trapezoid involves the object’s mass, height, and base lengths.
This concept has numerous applications in various fields, such as structural design, mechanical engineering, and aerospace engineering.
Importance, Moment of inertia of trapezoid
The moment of inertia is crucial in determining the stability and dynamic behavior of objects. It is used in:
- Calculating the natural frequencies of structures, such as buildings and bridges.
- Analyzing the stability of aircraft and spacecraft.
- Designing rotating machinery, such as flywheels and turbines.
FAQ Compilation
What is the formula for calculating the moment of inertia of a trapezoid?
The formula for calculating the moment of inertia of a trapezoid with height h, bases b1 and b2, and mass m is: (m/12) – (b1^2 + b1*b2 + b2^2) – h^2
How is the moment of inertia of a trapezoid used in engineering?
The moment of inertia is a crucial parameter in engineering for analyzing the rotational motion of objects. It is used in the design of flywheels, gears, and other rotating components to ensure stability and optimize performance.
What is the significance of the parallel axis theorem in calculating the moment of inertia of trapezoids?
The parallel axis theorem provides a convenient method for calculating the moment of inertia of a trapezoid about an axis parallel to its centroidal axis. It simplifies the calculations by allowing us to use the known moment of inertia about the centroidal axis.